maximum-height-by-stacking-cuboids

< Previous 　　　　　　　　　　　　　　　　 Next >

1691. Maximum Height by Stacking Cuboids (Hard)

Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

 

Example 1:

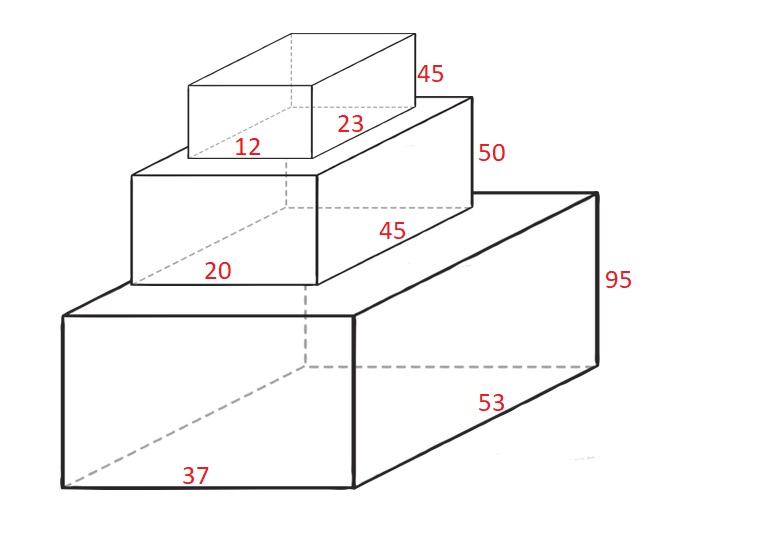
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

 

Constraints:

• n == cuboids.length
• 1 <= n <= 100
• 1 <= widthi, lengthi, heighti <= 100

Related Topics

[Array] [Dynamic Programming] [Sorting]

Hints

Hint 1

Does the dynamic programming sound like the right algorithm after sorting?

Hint 2

Let's say box1 can be placed on top of box2. No matter what orientation box2 is in, we can rotate box1 so that it can be placed on top. Why don't we orient everything such that height is the biggest?