README.md

< Previous 　　　　　　　　　　　　　　　　 Next >

1168. Optimize Water Distribution in a Village (Hard)

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i], or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[i] = [house1, house2, cost] represents the cost to connect house1 and house2 together using a pipe. Connections are bidirectional.

Find the minimum total cost to supply water to all houses.

 

Example 1:

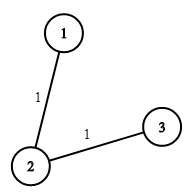
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: 
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

 

Constraints:

• 1 <= n <= 10000
• wells.length == n
• 0 <= wells[i] <= 10^5
• 1 <= pipes.length <= 10000
• 1 <= pipes[i][0], pipes[i][1] <= n
• 0 <= pipes[i][2] <= 10^5
• pipes[i][0] != pipes[i][1]

Related Topics

[Union Find] [Graph] [Minimum Spanning Tree]

Hints

Hint 1

What if we model this problem as a graph problem?

Hint 2

A house is a node and a pipe is a weighted edge.

Hint 3

How to represent building wells in the graph model?

Hint 4

Add a virtual node, connect it to houses with edges weighted by the costs to build wells in these houses.

Hint 5

The problem is now reduced to a Minimum Spanning Tree problem.