Skip to content

Specification Patterns for UPPAAL

Jump to bottom
Marc Carwehl edited this page Dec 16, 2021 · 2 revisions

Introduction

Introduction is taken from Gruhn and Laue, however, it might not be directly applicable to UPPAAL. Further useful literature for observer/test automata are Aceto et al. (1998) and Aceto et al. (2003).

Timed Observer Automata Intuitively, observers run in parallel with the model under verification. They reach a certain state if and only if some property can be violated in the model.

Safety To prove that such a property is true, it is sufficient to check that the observer cannot reach some location(s). A violation of the specification (a counterexample) is detected when the observer can reach such a location.

Liveness For liveness properties (like "every occurrence of P is followed by an occurrence of Q"), reasoning about infinite runs is necessary. As usual, we use acceptance conditions for this purpose: Some locations in the observer are marked as accepting locations. A counterexample is detected, if there is a non-Zeno run entering an accepting location infinitely often. (Intuitively, a non-Zeno run is one where it is forbidden to take infinitely many transitions in a finite amount of time.)

Conventions A violation of a specification is detected when a "bad" location can be reached in the observer. We call such locations error locations and mark them with the word ERROR.

Property Specification Patterns mapped to UPPAAL

The specification patterns and their mapping to LTL, CTL, MTL, TCTL, PLTL, and CSL can be found here. A discussion of some patterns can be found in Autili et al.. The initial patterns by Dwyer et al. can be found here. We first focus on the real-time property specification patterns by Konrad and Cheng while considering as well the untimed variants.

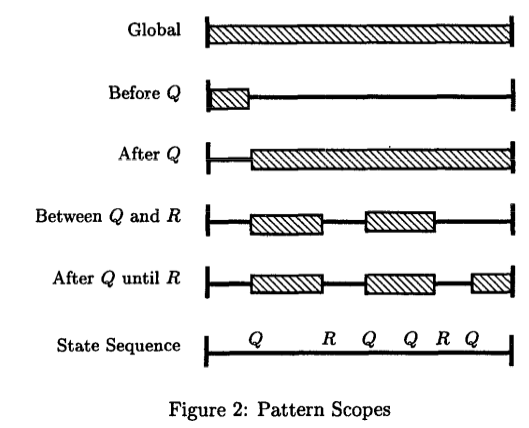
Scopes (Dwyer et al.)

Scopes

Equivalences

Use equivalences if it is useful or needed.

Name Property Equivalent to
Possibly E<> P --
Invariantly A[] P not E<> not P
Potentially always E[] P --
Eventually A<> P not E[] not P
Leads to P --> Q A[] (P imply A<> Q)

Events vs. State

Distinguish whether a property refers to an event or a state (proposition/formula). Event-based vs. State-based formalisms.

In UPPAAL, we may observe actions (events) and (shared) variables. Variables can be used to express state formulas.

State-based Property Specification Patterns

The state-based property specification patterns for UPPAAL can be found here

Techniques Enabling Verification with UPPAAL

According to Havelund et al., there are three techniques that address the limitations of UPPAAL in primarily supporting the verification of reachability properties. These techniques are the flag, the debt, and the observer techniques.

The Flag Technique

The flag technique enriches the system model with attributes that are set if specific states are or have been reached. Consequently, the attributes can be used in verifying properties that check the values of the attributes and thus whether the specific states have been reached or not.

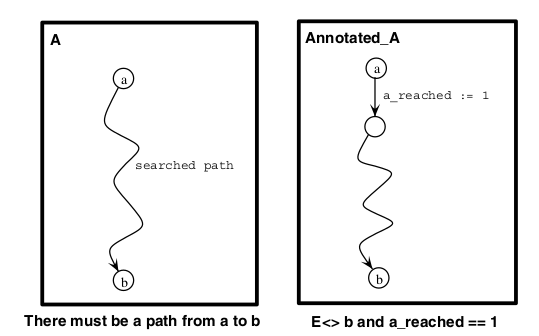
Flag Technique

Using the flag technique, we can either add an additional committed state "after" ("before") a and during the transition to this state (state a) the flag is set to 1. An alternative is to set the flag on all transitions leaving (entering) state a without adding any state to the model. A transition can have multiple updates, each separated by a comma from another update.

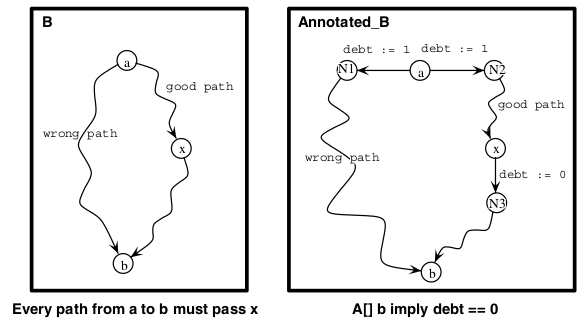
The Debt Technique

The debt technique extends the flag technique by not only considering when the attributes are set to a specific value but also when they are reset.

Debt Technique

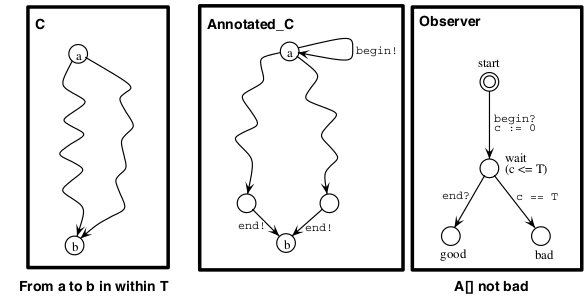
The Observer Technique

The observer technique adds a further automaton to the system model. The system model sends events to the observer automaton that uses these events to monitor the execution of the system. This technique allows us to measure/observe time since the observer can use its own clocks.

Considering the following figure. "When in node a, a begin! signal can be issued, telling the observer to start measure time. When reaching node b, no matter along which path, an end! signal is issued, telling the observer to stop measure time. The channel end is declared as urgent, hence it will be taken as soon as node b is reached (no time delays).

Observer Technique

Important notes

Self-loops to emit events

The use of the self-loop in state a to emit begin! can go wrong in our case. Assuming that the system is specified by more than one automaton, for instance, C and B. If C just entered state a and B is now in a committed state and able to synchronize with C on a transition leaving state a. In this case, the transition is fired that synchronizes both automata C and B (since the committed state in B must be involved in the next transition step) and not the self-loop transition begin!. Consequently, the system has reached the state a but the begin event has never been sent.

As an alternative we should add another committed state "before" a in automaton C. All transitions entering a will be redirected to the added state. The added state and a are connected by one transition emitting the event begin. This alternative is illustrated in the following figure. Instead of the generic channel begin, we use a specific channel (a_reached) since multiple of such channels are required when we want to observe more than one state (especially when more than one state is reached).

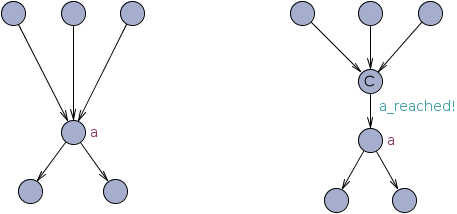
Observer Technique Example

In some cases, we can also add the state "after" a, however, while being in state a, time can potentially pass. In this case, we emit the event a_left denoting that the state a has been left.

Regular or Broadcast Channels

Events from the system model such as a_reached or a_left should be sent by broadcast channels, which simplifies the construction of the observer. In this case, the observer must only consider the events that are of interest and can ignore the other events because the sender (i.e., the system model) is not blocked (there is no deadlock) when there is no receiver to synchronize with. Thus, the observer must not be able to receive all potential "reached" or "left" events in each of its locations.

Adaptation of the System Model to Interact with Observers

To enable the interaction between the system model and an observer, the system model has to be adapted. Assuming that we are interested in observing when the system reaches and leaves location P, the system model is adapted as follows:

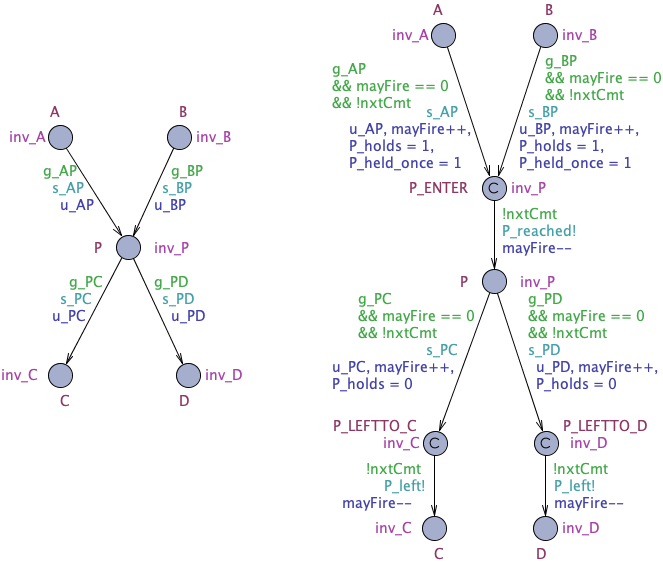
Observer Technique Specification

Potential self-loops of location P need not to be considered for the interaction since taking such a transition does not change anything with respect to entering and leaving P and therefore for holding P.

Special cases

  1. State P is an initial state so that it has no incoming transitions.
  2. State P is a state that has no outgoing transitions.
  3. Besides state P, we are also interested in observing its predecessor or successor state. In this case, the two adaptations of the system model overlap, one adaptation for observing state P and one for observing the predecessor or successor state.
  4. State P has self-loops. [Anything to be considered here?][Not really, those loops are not of interest to us and are therefore excluded from modification. They may be of interest when we consider Recurrence, though. But does P->P count as a recurrence?]

Semaphore Flags

As used by Li et al. we also want the system model to not be able to do anything while an automaton is in one of the pseudo-states we added in our modification process, i.e. P_ENTER. We cannot achieve this solely by using committed locations since there may be other committed locations in the system which can be exited while the system remains in a pseudo-state. Consider for example the following composition:

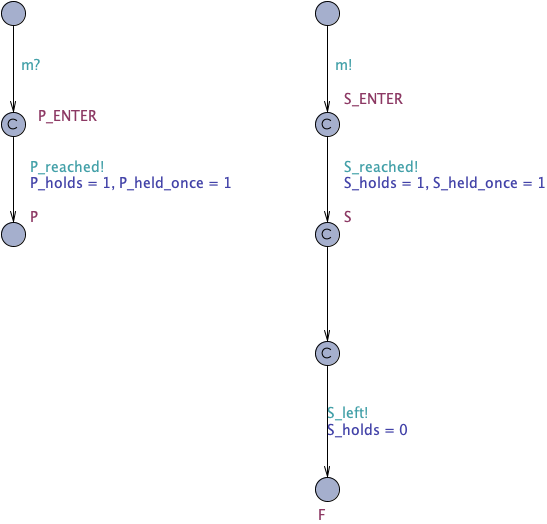
Composition without mayFire

The lefthand automaton can be in the pseudo-state P_ENTER while the automaton on the right is already in state F. To prohibit this behaviour, we use a flag mayFire which is increased when a pseudo-state is entered and decreased when it is left. Every transition that was present in the original system model has to be adapted: its guard will be changed so that it may only be fired when mayFire==0 holds:

Composition with mayFire

In the example above, S can only be left once P_ENTER is left.

Additionally, we have to make sure that some of the observer's transitions always have priority when they can be fired. Those transitions are marked committed. But similarly to the scenario described above this may not be sufficient. Another transition in the system model may be fired, for example some of the pseudo-states may be left before the observer has reacted to all the changes that happen in the pseudo-state. In the example below you can see that there is non-deterministic behaviour introduced: The observer on the right hand side can be either in state A or B depending whether first the automaton in the middle transitions to state F or whether the observer transitions to state A.

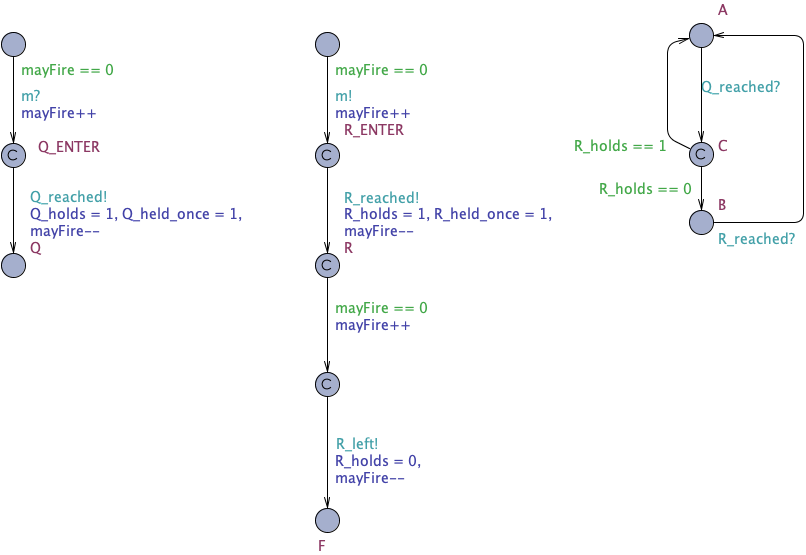
Composition without nxtCmt

To disable this unwanted behaviour, we introduce another semaphore variable: nxtCmt. This is a boolean, it will only be written by the observer, true if it wants to have priority, false otherwise. If this flag is true, no other transitions in the system (excluding the observer) may be enabled, not even those that we added in our modifications. We add the guard !nxtCmt to every transition.

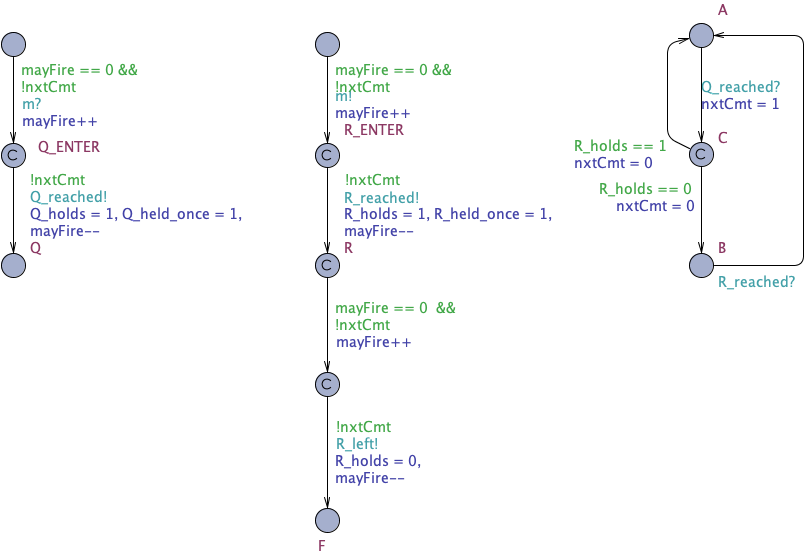
Composition with nxtCmt

Now the observer's behaviour is deterministic and it will end up in state A in every run.

Observing Events (instead of States)

So far, we were interested in observing when a specific state in the system model is reached or left. Additionally, we can observer events that occur in the system (model). For this purpose, two options can be considered: adaptation of the system model with use of observer automata, or the exclusive use of broadcast channels in the system model.

Adapt the System Model and Use of Observers

To observer when an event occurred in the system model, we adapt the model to emit another event directly after the event of interest occurred. For instance, if we are interested in observing the event e that is emitted in the system when going from state A to B. In this example, we add a committed state E between A and B to the model. Going from A to E the event e is emitted, going from E to B the event e_occurred is emitted through a broadcast channel.

Consequently, an observer can monitor the e_occurred event.

Exclusive Use of Broadcast Channels

To directly enable observers to monitor events (such as e) occurring in the system, the system must use only broadcast channels.

Consequently, when modeling/specifying the system---in the context of Safe.Spec the requirements---we must assure that the use of broadcast channels does not impact the system behavior. This is rather unrealistic. It becomes relevant when synchronizing two or more automata (processes) in the system on the same event. If we use broadcast channels, more than one automata consumes the event such that more than two automata can synchronize with one transition. Otherwise, with non-broadcast channels and if more than two automata can synchronize, two of these automata is selected non-deterministically to send respectively consume the event.

An alternative to broadcast channels could have been priorities among automata, for instance, in the system declaration Sys1, Sys2 < Observer gives the Observer a higher priority than Sys1 and Sys2 to synchronize and therefore to consume events. However, the observer must not consume events that are needed in the system so that it must send the event back to the system after consuming it. This makes the observer rather complicated. Moreover, UPPAAL does not support the verification of A<>, E[], and --> properties when using priorities (this might be possible with UPPAAL 4.1; see following comments).

Using broadcast channels has the following limitations:

  • In a broadcast synchronization one sender c! can synchronize with an arbitrary number of receivers c?. Any receiver than can synchronize in the current state must do so. If there are no receivers, then the sender can still execute the c! action/event, i.e., broadcast sending is never blocking (fire and forget). This implies an asynchronous communication for the sender.
  • UPPAAL cannot verify the deadlock predicate (A[] not deadlock) for models with priorities or models with guarded broadcast receivers.
  • The UPPAAL help for versions 4.0 and 4.1 states that "Notice that clock guards are not allowed on edges receiving on a broadcast channel." However, it seems that it works for version 4.1 but not for 4.0. According to the UPPAAL website, version 4.1.3 "[a]dded support for broadcasts with clock constraints on the receiver side". With the same version, the "liveness checker now supports models with priorities and broadcasts with clock constraints on the receiver side".

Conclusion

Consequently, the exclusive use of broadcast channels does not seem to be a good solution so that we will follow the same approach for observing events as we use for observing states: adapt the system model to emit additional events at appropriate locations in the model, which are consumed by observers.

Currently, we are focusing on state-based property specification patterns, that is, we are interested in observing when states are entered/reached or left or when the system is in a given state (i.e., the state holds), and thus consider event-based property specification patterns as future work.

Literature

Home

Specification Pattern Catalogue for UPPAAL

Evaluation

Clone this wiki locally