README.md

建立四叉树

难度：中等

https://leetcode-cn.com/problems/construct-quad-tree/

题目

给你一个 n * n 矩阵 grid ，矩阵由若干 0 和 1 组成。请你用四叉树表示该矩阵 grid 。

你需要返回能表示矩阵的 四叉树 的根结点。

注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 **接受 **。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

• val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
• isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：

1. 如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
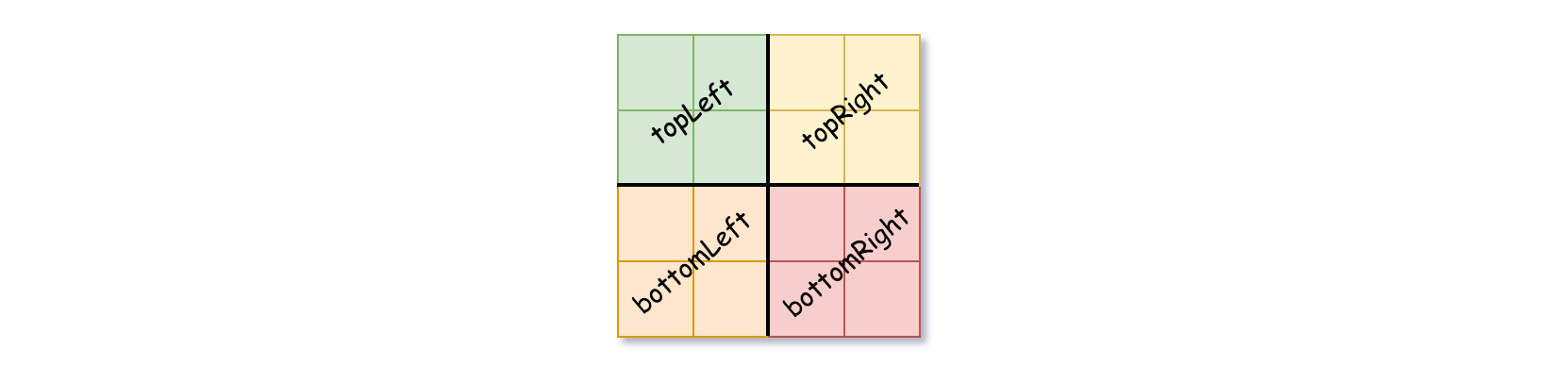
2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
3. 使用适当的子网格递归每个子节点。

如果你想了解更多关于四叉树的内容，可以参考 wiki 。

四叉树格式：

输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 `0 。

示例

示例 1：

输入：grid = [[0,1],[1,0]]
输出：[[0,1],[1,0],[1,1],[1,1],[1,0]]
解释：此示例的解释如下：
请注意，在下面四叉树的图示中，0 表示 false，1 表示 True 。

示例 2：

输入：grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
输出：[[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
解释：网格中的所有值都不相同。我们将网格划分为四个子网格。
topLeft，bottomLeft 和 bottomRight 均具有相同的值。
topRight 具有不同的值，因此我们将其再分为 4 个子网格，这样每个子网格都具有相同的值。
解释如下图所示：

示例 3：

输入：grid = [[1,1],[1,1]]
输出：[[1,1]]

示例 4：

输入：grid = [[0]]
输出：[[1,0]]

示例 5：

输入：grid = [[1,1,0,0],[1,1,0,0],[0,0,1,1],[0,0,1,1]]
输出：[[0,1],[1,1],[1,0],[1,0],[1,1]]

解题

递归

/**
 * 递归
 * @desc 时间复杂度 O(N²logN)  空间复杂度 O(logN)
 * @param grid
 * @returns
 */
export function construct(grid: number[][]): Node | null {
  return dfs(grid, 0, 0, grid.length, grid.length)

  function dfs(
    gird: number[][],
    row1: number,
    col1: number,
    row2: number,
    col2: number,
  ): Node | null {
    let same = true

    // 这一部分是否均为 1 或均为 0
    for (let i = row1; i < row2; i++) {
      for (let j = col1; j < col2; j++) {
        if (grid[i][j] !== grid[row1][col1]) {
          same = false
          break
        }
      }
      if (!same) break
    }

    if (same)
      return new Node(grid[row1][col1] === 1, true)

    const ret = new Node(
      true,
      false,
      dfs(gird, row1, col1, (row1 + row2) >> 1, (col1 + col2) >> 1),
      dfs(gird, row1, (col1 + col2) >> 1, (row1 + row2) >> 1, col2),
      dfs(gird, (row1 + row2) >> 1, col1, row2, (col1 + col2) >> 1),
      dfs(gird, (row1 + row2) >> 1, (col1 + col2) >> 1, row2, col2),
    )

    return ret
  }
}

递归 + 二维前缀和优化

/**
 * 递归 + 二维前缀和优化
 * @desc 时间复杂度 O(N²)  空间复杂度 O(N²)
 * @param grid
 * @returns
 */
export function construct2(grid: number[][]): Node | null {
  const len = grid.length
  const pre = new Array(len + 1).fill([]).map(() => new Array(len + 1).fill(0))
  for (let i = 1; i <= len; i++) {
    for (let j = 1; j <= len; j++) {
      pre[i][j]
      = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + grid[i - 1][j - 1]
    }
  }

  return dfs(grid, pre, 0, 0, grid.length, grid.length)

  function dfs(
    gird: number[][],
    pre: number[][],
    row1: number,
    col1: number,
    row2: number,
    col2: number,
  ): Node | null {
    const total = getSum(pre, row1, col1, row2, col2)
    if (total === 0)
      return new Node(false, true)
    else if (total === (row2 - row1) * (col2 - col1))
      return new Node(true, true)

    const ret = new Node(
      true,
      false,
      dfs(gird, pre, row1, col1, (row1 + row2) >> 1, (col1 + col2) >> 1),
      dfs(gird, pre, row1, (col1 + col2) >> 1, (row1 + row2) >> 1, col2),
      dfs(gird, pre, (row1 + row2) >> 1, col1, row2, (col1 + col2) >> 1),
      dfs(gird, pre, (row1 + row2) >> 1, (col1 + col2) >> 1, row2, col2),
    )

    return ret
  }

  function getSum(pre: number[][], row1: number, col1: number, row2: number, col2: number) {
    return pre[row2][col2] - pre[row2][col1] - pre[row1][col2] + pre[row1][col1]
  }
}