README.md

最大正方形

难度：中等

https://leetcode-cn.com/problems/maximal-square/

题目

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

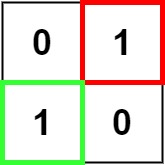
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

解题

暴力解法

/**
 * 暴力解法
 * desc 时间复杂度 O(min(M,N)²)  空间复杂度 O(1)
 * @param matrix
 * @returns
 */
export function maximalSquare(matrix: string[][]): number {
  let maxsize = 0

  if (matrix.length === 0 || matrix[0].length === 0) return maxsize

  const row = matrix.length
  const col = matrix[0].length

  for (let i = 0; i < row; i++) {
    for (let j = 0; j < col; j++) {
      if (matrix[i][j] !== '1') continue
      // 遇到一个 1 作为正方形的左上角
      maxsize = Math.max(maxsize, 1)
      // 计算可能的最大正方形边长
      const size = Math.min(row - i, col - j)
      for (let k = 0; k < size; k++) {
        // 判断新增的一行一列是否均为 1
        let flat = true

        if (matrix[i + k][j + k] === '0') break

        for (let l = 0; l < k; l++) {
          if (matrix[i + k][j + l] === '0' || matrix[i + l][j + k] === '0') {
            flat = false
            break
          }
        }

        if (!flat) break

        maxsize = Math.max(maxsize, k + 1)
      }
    }
  }

  return maxsize ** 2
}

动态规划

/**
 * 动态规划
 * desc 时间复杂度 O(MN)  空间复杂度 O(MN)
 * @param matrix
 * @returns
 */
export function maximalSquare2(matrix: string[][]): number {
  let maxsize = 0

  if (matrix.length === 0 || matrix[0].length === 0) return maxsize

  const row = matrix.length
  const col = matrix[0].length

  const dp: number[][] = new Array(row).fill([]).map(() => new Array(col).fill(0))

  for (let i = 0; i < row; i++) {
    for (let j = 0; j < col; j++) {
      if (matrix[i][j] === '1') {
        dp[i][j] = i === 0 || j === 0
          ? 1
          : Math.min(Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])) + 1

        maxsize = Math.max(maxsize, dp[i][j])
      }
    }
  }

  return maxsize ** 2
}