Merge pull request #314 from sandialabs/kuberry-gmls-explanation-update

- Updated README.md to work with Github markup as well as Doxygen
- Gave a more detailed overview of GMLS

Author: kuberry

README.md

@@ -8,18 +8,33 @@ This toolkit focuses on the 'on-node' aspects of meshless PDE solution and remap
 
 ### Generalized Moving Least Squares (GMLS)
 
-A GMLS problem requires the specification of a target functional 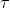![equation](https://latex.codecogs.com/gif.latex?\tau) (Compadre::TargetOperation), a reconstruction space 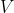![equation](https://latex.codecogs.com/gif.latex?V) (Compadre::ReconstructionSpace), and a sampling functional 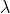![equation](https://latex.codecogs.com/gif.latex?\lambda) (Compadre::SamplingFunctional).
-
-The Compadre Toolkit is designed to efficiently assemble, factorize, and solve large batches of minimization problems having the form:
-
-![equation](https://latex.codecogs.com/png.latex?%5Cbg_white%20%5Clarge%20%5C%5C%20%5Cbegin%7Balign*%7D%20p%5E%7B*%7D%26%20%3D%26%20%5Cunderset%7Bp%20%5Cin%20V%7D%7B%5Ctext%7Barg%20min%7D%7D%5C%3B%5Cfrac%7B1%7D%7B2%7D%5Csum_%7Bj%3D1%7D%5EN%20%28%5Clambda_j%28u%29-%5Clambda_j%28p%29%29%5E%7B2%7D%5Comega%28%5Ctau%3B%5Clambda_j%29%5C%5C%5C%5C%20%26%26%5Ctau%28u%29%20%5Capprox%20%5Ctau%28p%5E%7B*%7D%29%20%5Cend%7Balign*%7D)
-<!---
-https://www.codecogs.com/latex/eqneditor.php
-\[\large \begin{align*}
-p^{*}& =& \underset{p \in V}{\text{arg min}}\;\frac{1}{2}\sum_{j=1}^N (\lambda_j(u)-\lambda_j(p))^{2}\omega(\tau;\lambda_j)\\\\
-&&\tau(u) \approx \tau(p^{*})
-\end{align*} \]
---->
+Here is a brief overview of the GMLS framework:
+
+Consider $\phi$ of function class $\mathbf{V}$ as well as a collection of samples $\Lambda = \\{\lambda_ i(\phi)\\}_ {i=1}^{N}$ (Compadre::SamplingFunctional) corresponding to a quasiuniform collection of data sites $\mathbf{X}_ h = \\{ \mathbf{x}_ i \\} \subset \mathbb{R}^d$ characterized by fill distance $h$. To approximate a given linear target functional $\tau_{\tilde{x}}$ (Compadre::TargetOperation) associated with a target site $\tilde{x}$, we seek a reconstruction $p \in \mathbf{V}_ h$, where $\mathbf{V}_ h \subset \mathbf{V}$ is a finite dimensional space (Compadre::ReconstructionSpace) chosen to provide good approximation properties, with basis $\mathbf{P} = \\{P\\}_{i=1}^{dim(V_h)}$. We perform this reconstruction in the following weighted $\ell_2$ sense:
+
+$$p = \underset{{q \in \mathbf{V}_ h}}{\mathrm{argmin}} \sum_{i=1}^N ( \lambda_i(\phi) -\lambda_i(q) )^2 \omega(\lambda_i,\tau_{\tilde{x}}),$$
+
+where $\omega$ is a locally supported positive function, $\omega = \Phi(|\tilde{x}-\mathbf{x}_i|)$ and $|\cdot|$ denotes the Euclidean norm. $\Phi(r,\epsilon)$ is selected by the user, having a parameter controlling the support of $\omega$.
+
+With an optimal reconstruction $p$ in hand, the target functional is approximated via $\tau_{\tilde{x}} (\phi) \approx \tau^h_{\tilde{x}} (\phi) := \tau_{\tilde{x}} (p)$.
+
+As an unconstrained $\ell_2$-optimization problem, this process admits the explicit form:
+
+
+$$\tau^h_{\tilde{x}}(\phi) = \tau_{\tilde{x}}(\mathbf{P})^\top \left(\Lambda(\mathbf{P})^\top \mathbf{W} \Lambda(\mathbf{P})\right)^{-1} \Lambda(\mathbf{P})^\top \mathbf{W} \Lambda(\phi),$$
+
+where:
+* $\tau_{\tilde{x}}(\mathbf{P}) \in \mathbb{R}^{dim(V_h)}$ is a vector with components consisting of the target functional applied to each basis function,
+* $\mathbf{W} \in \mathbb{R}^{N \times N}$ is a diagonal matrix with diagonal entries consisting of $\\{\omega(\lambda_i,\tau_{\tilde{x}})\\}_{i=1,...,N}$,
+* $\Lambda(\mathbf{P}) \in \mathbb{R}^{N \times dim(V_h)}$ is a rectangular matrix whose $(i,j)$ entry corresponds to the application of the $i^{th}$ sampling functional applied to the $j^{th}$ basis function,
+* and $\Lambda(\phi) \in \mathbb{R}^N$ is a vector consisting of the $N$ samples of the function $\phi$.
+
+Compadre forms and solves the GMLS problem for $\\{\alpha_i\\}$ used in the approximation $\tau^h_{\tilde{x}}(\phi) = \sum_{\mathbf{x}_i \in B^\epsilon(\tilde{x})} \alpha_i \lambda_i(\phi)$,
+where $B^\epsilon(\tilde{x})$ denotes the $\epsilon$-ball neighborhood of the target site $\tilde{x}$. 
+
+As such, GMLS admits an interpretation as an automated process for generating generalized finite difference methods on unstructured point clouds. Note that the computational cost of solving the GMLS problem amounts to inverting a small linear system which may be assembled using only information from neighbors within the support of $\omega$, and construction of such stencils across the entire domain is embarrassingly parallel.
+
+The Compadre Toolkit is designed to efficiently assemble, factorize, and solve large batches of GMLS problems.
 
 ## Wiki Information
 Details about building and using the Compadre toolkit can be found on the [Wiki](https://github.com/sandialabs/compadre/wiki).

doc/Doxyfile

@@ -926,7 +926,7 @@ INPUT_FILTER           =
 # filters are used. If the FILTER_PATTERNS tag is empty or if none of the
 # patterns match the file name, INPUT_FILTER is applied.
 
-FILTER_PATTERNS        = 
+FILTER_PATTERNS += "*.md=sed 's/\([^$]\)\$\([^$]*\)\$\([^$]\)/\1\\f$\2\\f$\3/g;s/\\{/\{/g;s/\\}/\}/g'"
 
 # If the FILTER_SOURCE_FILES tag is set to YES, the input filter (if set using
 # INPUT_FILTER ) will also be used to filter the input files that are used for
@@ -1500,7 +1500,7 @@ FORMULA_TRANSPARENT    = YES
 # The default value is: NO.
 # This tag requires that the tag GENERATE_HTML is set to YES.
 
-USE_MATHJAX            = NO
+USE_MATHJAX            = YES
 
 # When MathJax is enabled you can set the default output format to be used for
 # the MathJax output. See the MathJax site (see:
@@ -1523,7 +1523,8 @@ MATHJAX_FORMAT         = HTML-CSS
 # The default value is: http://cdn.mathjax.org/mathjax/latest.
 # This tag requires that the tag USE_MATHJAX is set to YES.
 
-MATHJAX_RELPATH        = http://cdn.mathjax.org/mathjax/latest
+# https was required to have it resolve on Github pages
+MATHJAX_RELPATH        = https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML
 
 # The MATHJAX_EXTENSIONS tag can be used to specify one or more MathJax
 # extension names that should be enabled during MathJax rendering. For example
@@ -1633,7 +1634,7 @@ EXTRA_SEARCH_MAPPINGS  =
 # If the GENERATE_LATEX tag is set to YES doxygen will generate LaTeX output.
 # The default value is: YES.
 
-GENERATE_LATEX         = YES
+GENERATE_LATEX         = NO
 
 # The LATEX_OUTPUT tag is used to specify where the LaTeX docs will be put. If a
 # relative path is entered the value of OUTPUT_DIRECTORY will be put in front of