-
Notifications
You must be signed in to change notification settings - Fork 2
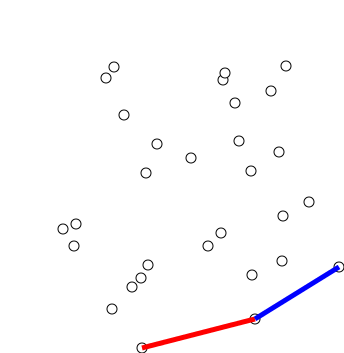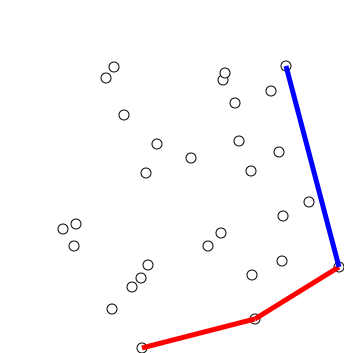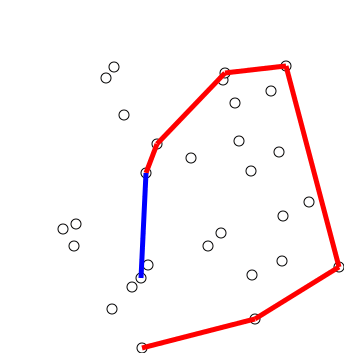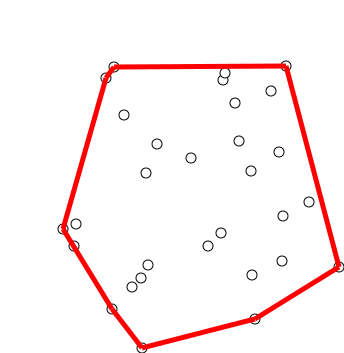
Geometric convex hull
Let points[0..n-1] be the input array.
-
Find the bottom-most point by comparing y coordinate of all points. If there are two points with the same y value, then the point with smaller x coordinate value is considered. Let the bottom-most point be P0. Put P0 at first position in output hull.
-
Consider the remaining n-1 points and sort them by the polar angle in counterclockwise order around points[0]. If polar angle of two points is the same, then put the nearest point first.
-
After sorting, check if two or more points have the same angle. If two more points have the same angle, then remove all same angle points except the point farthest from P0. Let the size of the new array be m.
-
If m is less than 3, return (Convex Hull not possible)
-
Create an empty stack ‘S’ and push points[0], points[1] and points[2] to S.
-
Process remaining m-3 points one by one. Do following for every point ‘points[i]’.
Keep removing points from the stack while the orientation of the following 3 points is not counterclockwise (or they don’t make a left turn).
a) Point next to top in stack
b) Point at the top of stack
c) points[I]
Push points[i] to S -
Print contents of S
struct point
{
double x, y;
point() { x = 0.0, y = 0.0; }
point(double xx, double yy) : x(xx), y(yy) {}
};
struct vec
{
double x, y;
vec() { x = 0.0, y = 0.0; }
vec(double xx, double yy) : x(xx), y(yy) {}
};
vec tovec (const point &A, const point &B) { return vec(B.x - A.x, B.y - A.y); }
double dist (const point &A, const point &B) { return hypot(A.x - B.x, A.y - B.y); }
double cross (const vec &A, const vec &B) { return A.x * B.y - B.x * A.y; }
double ccw (const point &p, const point &q, const point &r) { return cross(tovec(p, q), tovec(p, r)) > 0; }
double collinear (const point &p, const point &q, const point &r) { return fabs(cross(tovec(p, q), tovec(p, r))) < eps; }
int n;
point pivot;
vector<point> p;
bool grahamScan (const point &L, const point &R)
{
if (collinear(pivot, L, R))
return dist(pivot, L) - dist(pivot, R) < 0;
return ccw(pivot, L, R);
}
vector<point> findCVH (vector<point> P)
{
if (n <= 3)
{
if (!(P[0].x == P[n - 1].x && P[0].y == P[n - 1].y)) P.push_back(P[0]);
return P;
}
int P0 = 0;
for (int i = 1; i < n; ++i)
if (P[P0].y > P[i].y || (P[P0].y == P[i].y && P[i].x > P[P0].x)) P0 = i;
point tmp = P[0]; P[0] = P[P0]; P[P0] = tmp;
pivot = P[0];
sort(P.begin(), P.end(), grahamScan);
vector<point> S;
S.push_back(P[n - 1]);
S.push_back(P[0]);
S.push_back(P[1]);
int j = 2;
while (j < n)
{
int top = (int)S.size() - 1;
if (ccw(S[top - 1], S[top], P[j])) S.push_back(P[j++]);
else S.pop_back();
}
return S;
}